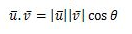SELAMAT DATANG DI MURAKOK.BLOGSPOT.CO.ID

semoga isi blog ini dapat menambah wawasan dalam pembelajaran matematika khususnya 

pada Geometri Analitik

PERSAMAAN BIDANG DATAR

Ax + By + Cz + D = 0 dimana A² + B² + C² ≠ 0
adalah persamaan pada koordinat kartesius  tiga dimensi

Jika diketahui dua bidang, yaitu A1x + B1y + C1z = D dan A2x + B2y + C2z = D, maka:

1.Jika θ adalah suatu sudut antara dua bidang ini, maka

2.      Dua bidang tersebut saling tegak lurus, apabila

3.      Dua bidang tersebut sejajar, apabila

4.      Dua bidang tersebut berimpitan, apabila

Jika d adalah jarak titik P(x1, y1, z1) ke bidang Ax + By + Cz = D maka

Persamaan bidang yang letak/posisinya istimewa.

• Ax = D adalah persamaan bidang yang sejajar dengan bidang yz, asal A tidak sama dengan nol
• By = D adalah persamaan bidang yang sejajar dengan bidang xz, asal B tidak sama dengan nol
• Cz = D adalah persamaan bidang yang sejajar dengan bidang xy, asal C tidak sama dengan nol
• x = 0 , y = 0 , z = 0 berturut-turut adalah persamaan bidang yz, bidang xz dan bidang xy
• Ax + By + Cz = 0 adalah persamaan bidang yang melalui titik asal o
• Ax + By = D adalah persamaan bidang yang sejajar dengan sumbu z
• Ax + Cz = D adalah persamaan bidang yang sejajar dengan sumbu y
• By + Cz = D adalah persamaan bidang yang sejajar dengan sumbu x

TUGAS

Apakah terdapat titik potong pada persamaan berikut:

Bidang P(1,2,3) Tegak Lurus dengan vektor n = <3,2,1>

Penyelesaian:

untuk

Titik potong terhadap sumbu x, maka z = 0

x = 6

sehingga (6,0,0)

Titik potong terhadap sumbu z, maka x = 0

z = 3

sehingga (0,0,3)

Titik potong terhadap sumbu x, maka y = z = 0

x = 4

sehingga (4,0,0)

Titik potong terhadap sumbu y, maka x = z = 0

y = -2

sehingga (0,-2,0)

Titik potong terhadap sumbu z, maka x = y = 0

z = 2

sehingga (0,0,2)

Dari persamaan bidang (1,2,3) tegak lurus vektor n = <3,2,1> didapatlah persamaannya:

Titik potong terhadap sumbu x, maka y = z = 0

x = 3,3

sehingga (3,3;0;0)

Titik potong terhadap sumbu y, maka x = z = 0

y = 5

sehingga (0,5,0)

Titik potong terhadap sumbu z, maka x = y = 0

z = 10

sehingga (0,0,10)

maka dapat disimpulkan bahwa tiga bidang yang terbentuk memiliki titik potong.

Vektor dalam ruang dimensi

dalam dimensi tiga suatu titik dinyatakan dengan tiga komponen, yaitu

1. absis 
2. ordinat
3. aplikat 

Misalnya B(x1, y1, z1). Vektor posisi (terhadap titik O) untuk titik B adalah a = < x1, y1, z1> = x1i, y1j, z1k.

PANJANG VEKTOR
Misalkan terdapat vektor a = < a1 , a2 , a3 > maka kita dapat mengetahui panjangnya dengan rumus :

PERKALIAN TITIK PADA VEKTOR
Jika u = < u1, u2, u3> dan v = < v1, v2, v3>, maka perkalian titiknya


Dengan θ adalah sudut yang dibentuk oleh u dan v dan serta 0 ≤ θ ≤ phi
Dari definisi diatass didaptkan rumus sudut yang dibentuk oleh vektor u dan v yaitu,


PERKALIAN VEKTOR
Jika u = < u1, u2, u3> dan v = < v1, v2, v3> maka perkalian kedua vektor adalah,


HASIL KALI SILANG DUA VEKTORPerkalian silang dua vektor a = a1i + a2j + a3k dan b = b1i + b2j + b3k didefinisikan sebagai berikut,




Dengan θ adalah sudut yang dibentuk kedua vektor dan u adalah vektor satun yang tegak lurus pada a dan b.