Vektor dalam bidang

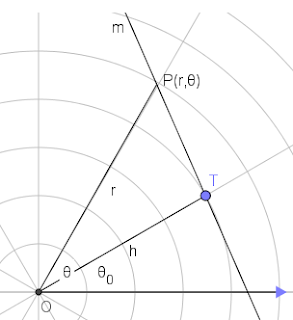
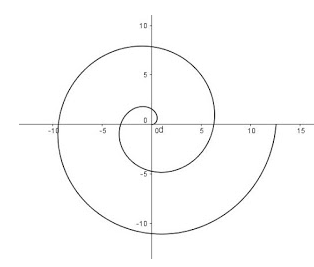
Vektor adala himpunan ruas garis berarah yang mempunyai besar dan arah yang sama.

Vektor digambarkan seperti anak panah (ruas garis berarah). Panjang ruas garis menyatakan besarnya vektor dan arah anak panah menyatakan arah vektor. 

pada gambar diatas, ruas-ruas garis berarah mempunyai besar dan arah sama, maka vektor itu dapat dinyatakan dengan simbol u atau dengan dua huruf besar. misalnya AB (diberi tanda panah diatas atau dibawah) ini dimaksudkan vektor dengan titik pangkal A dan titik ujung B. vektor ini dinamakan vektor bebas.

Suatu vektor yang titik pangkalnya tertentu dan vektor lainnya harus mempunyai titik pangkal tertentu, maka vektor dinamakan vektor posisi (vektor letak)

vektor di R2 adalah vektor yang terletak di satu bidang
atau Vektor yang hanya mempunyai dua komponen yaitu x dan y

Vektor di R3 adalah Vektor yang terletak di

ruang dimensi tiga  Vektor yang mempunyai tiga komponen yaitu x, y dan z

Penjumlahan Vektor
a. cara segitiga
untuk memperoleh jumlah dua vektor u dan v, yaitu u + v, gambarlah vektor v yang titik pangkalnya berimpit dengan titik ujung vektor u. Maka u + v adalah vektor yang menghubungkan titik pangkal u dan titik ujung vektor v .

b. cara jajarangenjang

cara ini dengan menggambarkan vektor v sehingga titik pangkalnya berimpit dengan titik pangkal vektor u. selanjutnya dibuat garis dari ujung u sejajar v dan garis dari ujung v sejajar u, sehingga didapat bangun jajaran genjang. Maka u + v adalah vektor yang bertitik  pangkal berimpit dengan titik pangkal u dan berimpit diagonal jajaran genjan

Pengurangan Vektor
Pengurangan vektor aadalah u - v = u + (-v). sehingga digambarkan sebagai berikut :

Teorema :

untuk sebarang vektor u, v dan w dan sebarang skalar a dan b berlaku sifat-sifat berikut 

perkalian vektor

Teorema hasil kali titik

untuk sebarang vektor u, v dan w dan k suatu skalar berlaku sifat-sifat berikut ini 

persamaan parametrik

Bentuk umum persamaan parametri dari suatu kurva bidang adalah

kurva bidang ada 4 macam, yaitu:
(1) Kurva tertutup sederhana
(2) Kurva tertutup tidak sederhana
(3) Kurva tidak tertutup sederhana
(4) Kurva tidak terp dan tidak sederhana

Suatu kruva dikatakan tertutup apabila titik ujung pangkalnya berimpit. Suatu kurva dikatakan sederhana, apabila kurva tersebut tidak mempunyai titik potong (dua nilai atau lebih memberikan titik titik yang sama).

Persamaan parametrik suatu kurva dapat dinyatakan ke dalam persamaan Kartesius dengan cara melenyapkan parameternya. Untuk meletutunyapkan parameternya, kadang menggunakan cara substitusi atau menentukan hubungan dari parameternya.
Setiap persamaan Kartesius dapat dinyatakan sebagai persamaan parameternya dan sebaliknya kadang kadang suatu kurva dapat dinyatakan dengan persamaan parameternya yang sederhana, tetapi jika dinyatakan dalam persamaan Kartesius menjadi lebih rumit. Kurva dari suatu persamaan parametrik merupakan kurva berarah.

Persamaan kutub dan grafiknya

Grafik garis lurus yang melalui titik asal dan membentuk sudut θ dengan sumbu kutub.

garis lurus m yang berjarak d dari kutub (d>0) dann θ adalah sudut antara sumbu kutub dan garis yang tegak lurus dari kutub pada garis m. tentukan persamaan kutub untuk garis m

Dengan mengambil sembarang titik P(r,θ) pada garis m. Pada segitiga OTP dengan <POT = θ-θo maka berlaku

cos (θ-θo) = d/r
r = d / cos (θ-θo)

Karena P (r, θ) sembarang titik pada garis m dan berlaku hubungan tersebut, maka untuk setiap titik pada garis m berlaku hubungan itu.

Jadi persamaan kutub untuk garis lurus yang berjarak d dari kutub dan normalnya membentuk sudut θo dengann sumbu kutub adalah

Limason dan Kardioda

     r = a ± b cos θ , r = a ± b sin θ dengan a,b konstanta yang positif

Lemniskat

     r²= ± a cos 2θ,  r²= ± a sin 2θ dengan a suatu konstanta positif

 Mawar

    r=  a cos nθ , r=  a sin nθ dengan a suatu konstanta

Spiral

     r = aθ dengan a konstanta

Koordinat kutub

Dalam sistem koordinat kutub hanya menggunakan sebuah sinar garis sebagai patokan muka, biasanya garis ini digambar mendatar dan mengarah ke kanan seperti tampak pada gambar dibawah ini. Garis ini dinamakan sumbu kutub, sedangkan titik pangkalnya yang biasa diberi nama dengan huruf O disebut Kutub atau titik asal.

Sebuah titik P  dinyatakan kedudukan oleh jarak titik O ke P dan sudut antara garis OP dan sumbu kutub, maka (r,θ) adalah sepasang koordinat kutub dari titik P. Selanjutnya r disebut jari-jari penunjuk dari P atau radius vektor dari P. Sedangkan θ disebut argumen dari P atau sudut kutub dari P

Hubungan sistem koordinat kartesius dan sisitem koordinat kutub adalah

Koordinat Kutub	Koordinat Kartesius
P(r,θ)	P(x,y)
r = f(θ)	y = f(x)

CONTOH 1 

di ketahui koordinat kartesius A(1,2)

ditanya koordinat kutub

  CONTOH 2

Diketahui : <xOB = 135⁰  dan r = 4                                   

Ditanya : Tentukanlah koordinat B pada koordinat kartesius.

Penyelesaian :

x = r cos θ                                  y = r sin θ

x = 4 cos 135⁰                                     y = 4 sin 135⁰

x = 4 (-0,707)                             y = 4 (0,707)

x = -2,828                                  y = 2,828

Sehingga koordinat kartesius B adalah (-2,828 ; 2,828)

Parabola

Parabola adalah himpunan titik-titik yang berjarak sama dari suatu titik dan suatu garis tertentu. 

1. Persamaan puncak parabola adalah y=2px

2. Jika titik O(0,0) adalah puncak parabola

3. F (1/2p, 0) adalah titik api.

4. Garis x = -1/2 p adalah garis arah(direktris), p disebut parameter parabola

5. Eksentrisitas numerik parabola adalah e = 1

Untuk parabola dengan puncak p(a,b) dan sumbu simetrinya sejajar sumbu x persamaannya adalah

 Jika sumbu simetri berimpit dengan sumbu x, titik puncak parabola berimpit dengan titik O  parabolanya terletak pada setengah bidang sebelah kiri, maka persamaan parabolanya

Jika sumbu simetri berimpit dengan sumbu y, titik puncak parabola berimpit dengan titik O parabolanya terletak pada setengah bidang sebelah atas maka persamaan parabolanya adalah

Jika sumbu simetri berimpit dengan sumu y, titik puncak parabola berimpit dengan titik O dan parabolanya terletak pada setengah bidang sebelah bawah, maka persamaan parabolanya adalah

Garis singgung parabola

Garis singgung di suatu titik pada parabola membagi dua sama besar sudut antara garis yang menghubungkan titik singgung dengan titik api dan garis yang melalui titik singgung sejajar dengan sumbu x.

pada parabola 

persmaan garis singgung nya adalah

Hiperbola

Hiperbola adalah tempat kedudukan titik-titik yang selisih jaraknya terhadap dua titik tertentu selalu tetap. Dua titik tertentu itu disebut fokus hiperbola.Jika jarak kedua titik tertentu tersebut adalah d, maka selisih jarak tersebut leih kecil dari d. Untuk setiap iik T berlaku | TF2-TF1 | = d

F1 dan F2 adalah titik fokus hiperbola

C dan B adalah titik-titik puncak

Misalkan titik-titik fokus, F1,F2 pada sumbu x dan sumbu dari F1F2 adalah sumbu y. Jika |F1F2| = 2c maka F1(-c,0) dan F2(c,0). Misalkan selisih jarak yang tetap itu adalah 2a dengan a < c.

Dengan P(x,y) sebarang titik yang memenuhi definisi, yaitu:

ellips

ellips adalah himpunan semua titik yang jumlah jaraknya terhadap dua titik tertentu tetap besarnya .tempat kedudukan titik yang jumlah jaraknya terhadap dua titik tertentu adalah sama/tetap .dua titik tertentu tersebut di kenal dengan istilah titik fokus atau titik api.jumlah jarak yang tetap tersebut = 2a,a>0

• F1 dan F2 di sebut titik titik api atau fokus
• AB di sebut sumbu mayor
• CD di sebut sumbu pendek
• titik titik A,B, dan C di sebut puncak ellips 
• Ti merupakan sembarng titik pada ellips

Misal titi fokus F1,F2 pada sumbu x dan sumbu dari F1F2 adalah sumbu y. jika |F1F2|=2c maka F1(c,0) dan F2(-c,0). misalkan jumlah jaran yang tetap itu adalah 2a dengan a>c

Ambil T(x,y) sebarang titik yang memenuhi Definisi, yaitu :

maka di dapat persamaan ellips adalah

Untuk sumbu utama horizontal, jika bergerak persimpangan sumbu x dan y ke titik (h,k) akan kita dapatkan:

garis singgung ellips

Garis singgung disuatu titik pada elips yang membagi dua sama besar sudut antara garis penghubung.

maka persamaan ellips dengan gradien m

dan untuk persamaan garis singgung di titik pusat P(α,β)